Sorites paradox
The sorites paradox (from Ancient Greek: σωρείτης sōreitēs, meaning "heaped up") is a paradox that arises from vague predicates. The paradox of the heap is an example of this paradox which arises when one considers a heap of sand, from which grains are individually removed. Is it still a heap when only one grain remains? If not, when did it change from a heap to a non-heap?
Contents |
Variations of the paradox
Paradox of the heap
The word "sorites" derives from the Greek word for heap. The paradox is so named because of its original characterization, attributed to Eubulides of Miletus.[1] The paradox goes as follows: consider a heap of sand from which grains are individually removed. One might construct the argument, using premises, as follows:
- 1,000,000 grains of sand is a heap of sand (Premise 1)
- A heap of sand minus one grain is still a heap. (Premise 2)
Repeated applications of Premise 2 (each time starting with one fewer grains), eventually forces one to accept the conclusion that a heap may be composed of just one grain of sand (and consequently, if one grain of sand is still a heap, then removing that one grain of sand to leave no grains at all still leaves a heap of sand; indeed a negative number of grains must also form a heap[2]).
On the face of it, there are some ways to avoid this conclusion. One may object to the first premise by denying 1,000,000 grains of sand makes a heap. But 1,000,000 is just an arbitrarily large number, and the argument will go through with any such number. So the response must deny outright that there are such things as heaps. Peter Unger defends this solution. Alternatively, one may object to the second premise by stating that it is not true for all heaps of sand that removing one grain from it still makes a heap. Or one may accept the conclusion by insisting that a heap of sand can be composed of just one grain, and solely deny the further conclusions regarding zero-grain or negative-grain-number heaps.
Variations
This paradox can be reconstructed for a variety of predicates, for example, with "tall", "rich", "old", "blue," "bald," and so on. Bertrand Russell argued[3] that all of natural language, even logical connectives, is vague; moreover, representations of propositions are vague. However, most views do not go that far, but it is an open question.
Proposed resolutions
Setting a fixed boundary
A common first response to the paradox is to call any set of grains that has more than a certain number of grains in it a heap. If one were to set the "fixed boundary" at, say, 10,000 grains then one would claim that for fewer than 10,000, it's not a heap; for 10,000 or more, then it is a heap.
However, such solutions are unsatisfactory as there seems little significance to the difference between 9,999 grains and 10,000 grains. The boundary, wherever it may be set, remains as arbitrary and so its precision is misleading. It is objectionable on both philosophical and linguistic grounds: the former on account of its arbitrariness, and the latter on the ground that it is simply not how we use natural language. A more acceptable solution is to call any collection of multiple grains (two or more) a heap.
Unknowable boundaries (or Epistemicism)
Timothy Williamson and Roy Sorensen hold an approach that there are fixed boundaries but that they are necessarily unknowable.
Supervaluationism
Supervaluationism is a semantics for dealing with irreferential singular terms and vagueness. Consider the sentence 'Pegasus likes licorice' in which the name 'Pegasus' fails to refer. What should its truth value be? There is nothing in the myth that would justify any assignment of values to it. On the other hand, consider 'Pegasus likes licorice or Pegasus doesn't like licorice' which is an instance of the valid schema 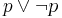 (i.e. '
(i.e. ' or not-
or not- '). Shouldn't it be true regardless of whether or not its disjuncts have a truth value? According to supervaluationism, it should be.
'). Shouldn't it be true regardless of whether or not its disjuncts have a truth value? According to supervaluationism, it should be.
Precisely, let  be a classical valuation defined on every atomic sentence of the language
be a classical valuation defined on every atomic sentence of the language  , and let
, and let 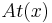 be the number of distinct atomic sentences in
be the number of distinct atomic sentences in  . Then there are at most
. Then there are at most 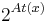 classical valuations defined on every sentence
classical valuations defined on every sentence  . A supervaluation
. A supervaluation  is a function from sentences to truth values such that,
is a function from sentences to truth values such that,  is super-true (i.e.
is super-true (i.e.  ) if and only if
) if and only if 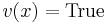 for every
for every  ; likewise for super-false. Otherwise,
; likewise for super-false. Otherwise, 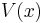 is undefined—i.e. exactly when there are two valuations
is undefined—i.e. exactly when there are two valuations  and
and 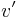 such that
such that 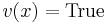 and
and  .
.
For example, let 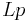 be the formal translation of 'Pegasus likes licorice'. Then there are exactly two classical valuations
be the formal translation of 'Pegasus likes licorice'. Then there are exactly two classical valuations  and
and 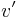 on
on 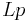 , viz.
, viz. 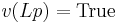 and
and 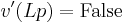 . So
. So 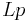 is neither super-true nor super-false.
is neither super-true nor super-false.
Truth gaps, gluts, and many-valued logics
Another approach is to use a multi-valued logic. From this point of view, the problem is with the principle of bivalence: the sand is either a heap or is not a heap, without any shades of gray. Instead of two logical states, heap and not-heap, a three value system can be used, for example heap, unsure and not-heap. However, three valued systems do not truly resolve the paradox as there is still a dividing line between heap and unsure and also between unsure and not-heap. The third truth-value can be understood either as a truth gap or as a truth glut.
Alternatively, fuzzy logic offers a continuous spectrum of logical states represented in the unit interval of real numbers [0,1]—it is a many-valued logic with infinitely-many truth-values, and thus the sand moves smoothly from "definitely heap" to "definitely not heap", with shades in the intermediate region. Fuzzy hedges are used to divide the continuum into regions corresponding to classes like definitely heap, mostly heap, partly heap, slightly heap, and not heap.
Hysteresis
Another approach is to use hysteresis—that is, knowledge of what the collection of sand started as. Equivalent amounts of sand may be called heaps or not based on how they got there. If a large heap (indisputably described as a heap) is slowly diminished, it preserves its "heap status" to a point, even as the actual amount of sand is reduced to a smaller number of grains. For example, let's say 500 grains is a pile and 1,000 grains is a heap. There will be an overlap for these states. So if you are reducing it from a heap to a pile, it is a heap going down until, say, 750. At that point you would stop calling it a heap and start calling it a pile. But if you replace one grain, it would not instantly turn back into a heap. When going up it would remain a pile until, say, 900 grains. The numbers picked are arbitrary; the point is that the same amount can be either a heap or a pile depending on what it was before the change. A common use of hysteresis would be the thermostat for air conditioning: the AC is set at 77 °F and it then cools down to just below 77 °F, but does not turn on again instantly at 77.001 °F—it waits until almost 78 °F degrees, to prevent instant change of state over and over again.[4]
Group consensus
One can establish the meaning of the word "heap" by appealing to group consensus. This approach claims that a collection of grains is as much a "heap" as the proportion of people in a group who believe it to be so. In other words, the probability that any collection is considered a heap is the expected value of the distribution of the group's views.
A group may decide that:
- One grain of sand on its own is not a heap.
- A large collection of grains of sand is a heap.
Between the two extremes, individual members of the group may disagree with each other over whether any particular collection can be labelled a "heap". The collection can then not be definitively claimed to be a "heap" or "not a heap". This can be considered an appeal to descriptive linguistics rather than prescriptive linguistics, as it resolves the issue of definition based on how the population uses natural language.[5] Indeed, if a precise prescriptive definition of "heap" is available then the group consensus will always be unanimous and the paradox does not arise.
See also
References
- ^ (Barnes 1982), (Burnyeat 1982), (Williamson 1994)
- ^ Dolev, Y. (2004). "Why Induction Is No Cure For Baldness". Philosophical Investigations 27 (4): 328–344. doi:10.1111/j.1467-9205.2004.t01-1-00230.x.
- ^ Russell, Bertrand (June 1923). "Vagueness". The Australasian Journal of Psychology and Philosophy 1 (2): 84–92. doi:10.1080/00048402308540623. ISSN 1832-8660. http://cscs.umich.edu/~crshalizi/Russell/vagueness/. Retrieved November 18, 2009. Shalizi's 1995 etext is archived at archive.org and at WebCite.
- ^ Raffman, D. (2005). "How to understand contextualism about vagueness: reply to Stanley". Analysis 65 (287): 244–248. doi:10.1111/j.1467-8284.2005.00558.x.
- ^ North, Ryan (August 28, 2009). "August 28th, 2009 - awesome fun times!". Dinosaur Comics. http://www.qwantz.com/index.php?comic=1541. Retrieved 9 June 2010.
- Black, Max (1970). Margins of Precision. Ithaca,Ny: Cornell University Press. ISBN 0801406021.
- Barnes, J. (1982). "Medicine, experience and logic". In J. Barnes, J. Brunschwig, M.F. Burnyeat and M. Schofield. Science and Speculation. Cambridge: Cambridge University Press
- Burns (1991). Vagueness : an investigation into natural languages and the Sorites Paradox. Dordrecht: Kluwer Academic Publishers. ISBN 0-792-314891.
- Burnyeat, Myles (1982). "15. Gods and heaps". In M. Schofield and M.C. Nussbaum. Language and Logos. Cambridge: Cambridge University Press. pp. 315–
- Gerla (2001). Fuzzy logic : mathematical tools for approximate reasoning. Dordrecht, Netherlands: Kluwer Academic Publishers. ISBN 0-7923-6941-6.
- Goguen, J. A. (1969). "The logic of inexact concepts". Synthese 19 (3–4): 325–373. doi:10.1007/BF00485654.
- Williamson, Timothy (1994). Vagueness. London: Routledge.
External links
- Sorites paradox entry in the Stanford Encyclopedia of Philosophy by Dominic Hyde.